*stevengould.org*

Support this site:

* DRAFT *
Variance Reduction Techniques applied to large scale simulation models

Steven R. Gould

Formerly with
Royal Aerospace Establishment
Farnborough

[Although the work was carried out at RAE, Farnborough this was back in the summer of 1989. The author can now be contacted via e-mail. Note that this is only a draft - any comments would be more than welcome. Thanks!]

ABSTRACT

Large scale simulation models are often very complex and require long run-times. As a result, it is often desirable to make them more precise so that a greater degree of accuracy may be achieved without increasing these times. One way in which this may be done is by the use of Variance Reduction Techniques. This paper discusses the application of a number of these techniques to large scale models at the Royal Aerospace Establishment (RAE), Farnborough. Where variance reductions were poor, it suggests why this may be so and gives possible ways of improving these. A modification to the antithetic variates variance reduction technique is proposed to make it more suitable to large, complex models. Of particular interest is the successful application of martingales and control variates to two of the models.

INTRODUCTION

Many simulation studies aim to estimate the steady-state mean of some performance parameter. The usual method of increasing the accuracy of such estimates is simply to increase the number N of replications of the model. However, the precision of such stochastic simulation estimators only increases as the square root of the computational effort; ie. .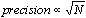

In the situations studied in this paper, it is not desirable to continue increasing N indefinitely until the required accuracy is reached simply because the time required would be unacceptable. It is therefore necessary to look at ways of increasing the accuracy of the estimators without increasing the number of replications N. Such methods of manipulating the simulation so as to improve the accuracy of the estimators are known as Variance Reduction Techniques (VRTs).

BACKGROUND

Part of the RAEs work involves studying the effectiveness of various methods of air-to-ground attacks on mobile targets. A major part of this process makes use of a number of large scale simulation models. The major one studied in this paper simulates the end-game effectiveness of different weapon systems upon different target arrangements.

The model studied is of a replicative nature -- that is one run (or replication) of the model simulates one possible outcome from start to finish. To obtain a reasonable estimate of the parameter of interest, it is therefore necessary to perform a (possibly large) number of such replications and take, say, the mean of these observations. This is in contrast to a regenerative simulation model where some number, n, of runs/trials are made by dividing one long run into n independent runs post hoc.

INITIAL RESULTS ON A MORE COMPLEX MODEL

An earlier study[1] by the author on a similar, but more complex model provided valuable experience and results on which to base this work. The main points resulting from this earlier work are summarised below:

Antithetic Variates[2]

These gave some promising variance reductions for small test runs with n = 2 x 20 antithetic pairs. However, as n was increased the variance reductions seemed to disappear and some large variance productions were observed. The reason for such disappointing results was found to be that the antithetic pairs were not strongly negatively correlated as required. Due to the great complexity of the model, the long chain of random events seemed to remove any negative correlation "created", leaving antithetic runs with an almost random correlation.

For this reason the antithetic variates VRT is not really suited to large, complex models. However better results may be possible in such models if it is possible to apply modified antithetic variates as described below.

Modified Antithetic Variates

We are interested in outcomes resulting from the latter stages of the implementation. It may therefore be more appropriate to use random numbers a₀, a₁, ..., a_k-1 for the earlier stages of the simulation, for both antithetic runs; then, only after a series of interesting events occur, switch over to using a_k, a_k+1, ..., a_K and (1 - a_k), (1 - a_k+1), ..., (1 - a_K) as the random numbers for the antithetic pairs. For example, if we wait until the aircraft has released it weapon(s) before applying antithetic random numbers, then the result may be more precise.

This may seem a strange idea to grasp at first, because we are, in effect, ensuring a positive correlation. However this only continues up to some predetermined point, after which the usual antithetic variates VRT is applied. By doing this we ensure that two similar circumstances have antithetic variates applied to them, hence the corresponding outcomes should be more negatively correlated.

Consider the case where we wait until a weapon is released before applying antithetic variates. We are really concerned with a sub-model of the simulation; one which models the actual weapon attack. Since other "external" factors need to be considered when evaluating any system, it is necessary to simulate any important events up to this point. We then enter the sub-model with a random set of inputs which is the same for both antithetic runs. Performance within the sub-model is then subjected to the antithetic variates VRT, where the outcomes are more strongly (negatively) correlated than before. The result will be a more precise estimate of the performance parameters of interest. This process may be illustrated as :

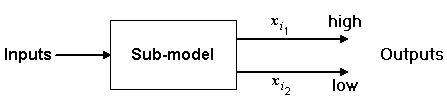
Figure 1.

Justification of this idea lies in the fact that antithetic variates can produce quite significant variance reductions when applied to one random event. Good variance reductions may also be possible with two or three random events happening in series, as is the case in many academic examples. However, as the chain of random events is extended, the negative correlation between outcomes is reduced until the point where, after a long sequence of such events, there is virtually zero correlation between the runs. This will be the case particularly in large complex models such as those studied here, and is illustrated by the poor results obtained.

By cutting down the sequence of events to consider only those of greatest interest, it is possible to maintain a good negative correlation between runs. Hence, we have justified the consideration of some small sub-model, to which the antithetic variates VRT is applied, as a means of improving the effectiveness of the technique.

Correlated Sampling[3,4]

This gave the best variance reductions of all VRTs applied to this model and, in fact, was one of the easiest to implement. The worst variance reduction was a reasonable +14.2%, however this was with only 2 sets of 40 observations. For larger numbers of observations (say >= 100), the worst variance reduction was a good +23.7%. These worst cases contrasted with variance reductions of up to 88%. Typically, though, variance reductions of about 50-55% were usual.

Control Variates[5]

Control variables were constructed reflecting the level of attrition on the aircraft carrying the weapon systems. Provided the number of replications (n) was large compared to the number of control variables (m=10), then variance reductions were observed for all estimators. Significant bias seemed to be associated with the larger variance reductions (of up to 51.6%) achieved, perhaps as a result of performing too few replications. However using Jackknifed regression[6] to provide more robust estimates had only a very small affect on the already large variance reductions. In contrast, where there had been only small variance reductions (of between 1.5% and 9.0%), the bias in the estimators was insignificant - the control variables used were not so relevant to these performance parameters.

Overall, stable variance reductions were achieved provided n >> m, however the magnitude of these improvements was slightly disappointing. The reason for only small variance reductions was due mainly to the choice of control variables and also due to a "quirk" in the model. If good control variables were found then we could of expected greater variance reductions.

Martingales[7]

Martingales reflecting detection/hit/kill probabilities were used and gave some poor results. The main reason for this was thought to be that they try to reduce random variation in the results, whereas this only makes up a small part of the overall variation - the main source being from the distribution and density of targets relative to submunition release points. The martingales used did not even attempt to reduce this. A later observation suggested that a relatively small number of replications relative to the number of martingales may also have contributed to the poor results.

If the main source of variation can however be identified, more suitable martingales may be constructed. In such cases, it was felt that martingales, like the control variables on which they are based, could offer potentially large variance reductions.

FURTHER ANALYSIS

Based upon these initial results, it was decided to look at another similar model which simulated attacks of different weapon systems from target acquisition through to weapon impact. This model was often used for large numbers of runs with many different scenarios and, as a result, an improvement in accuracy was desirable.

Modified antithetic variates

The first stage in the implementation of modified antithetic variates involved applying the full antithetic variates VRT. This meant changing the model so that every process within it used a different random number stream.

Once the full antithetic variates VRT had been implemented, it was necessary to identify where the main source of variance arose. From previous work on the more complex model, it had been found that the main variance was not due to randomness in the detection, hit or kill of individual targets, but occurred at some stage before this. As a result it was decided to try implementing modified antithetic variates from the dispense of submunitions onwards. This gave small improvements over normal antithetic variates, however the results were still disappointing with small variance reductions and even, in some cases, variance productions.

Other points in the model were tried, for example, dispenser flyout. However similarly poor results were observed. The reason behind this was that the major source of variation had not been identified and, as a result, good negative correlations between the runs were not being achieved. Consequently, it was decided that the model was too complex for antithetic variates (and even modified antithetic variates) to be of any significant use, and that time spent persueing it would be better spent looking at other techniques.

Martingales and Control Variates

Table 1 (below) shows the development in the selection of martingales and control variates for the model of weapon system 1. When a variable likely to be a good control variable / martingale was found it was tested on the base case along with the current "best" set of variables. If any variance production was detected in targets hit/killed then this variable was labelled as unsuitable and dropped from further tests.

Table 1. Development in the selection of Martingales and Control Variables

                               PARAMETER 1    PARAMETER 2    PARAMETER 3
                               std.  jack-    std.  jack-    std.  jack-
                                    knifed         knifed         knifed

Dispenser/submunition   1 M     2.1    2.1     4.7    5.0    +0.3   +0.2
   reliability
Detection/Hits/Kills    6 M     2.4    2.5    22.4   22.8    +0.0   -0.1
   martingales 
Aircraft positioning    1 CV   32.4   35.0    46.5   48.8    -0.5   -0.2

Pilot steering error    1 CV   (2.2)  (2.0)  (22.3) (22.4)  (-0.2) (-0.6)

Dispenser errors        4 CV  (32.0) (34.1)  (46.1) (48.0)  (-0.2) (-1.2)

Target separation       2 CV  (32.1) (34.5)  (46.3) (48.5)  (-1.0) (-1.2)

Notes:

Figures in brackets indicate variance production over the previous "best" set of control variables; consequently the new control variable(s) were dropped from further tests.
All results here are for the base case only, however relative variance reductions would be similar for other cases.
M indicates martingale; CV indicates control variable in column 2 of the table.

Note that it would have been easy to find several more possible martingales and control variables, however these would only have been relevant to certain scenarios. The set described below however was generally applicable to all runs of the weapon system 1 model.

Dispenser / Submunition reliability martingale

This martingale reflects the reliability of the dispensers and submunitions in weapon system 1. In any one replication, it sums all attempts to release dispensers and submunitions, in the one martingale.

Let the dispensers have a reliability (ie. probability of working) of rel_d and submunitions a reliability of rel_s. Assume there are n_s submunitions per dispenser, then we can construct a martingale in the following way.

At the beginning of each replication the martingale is initialised to zero. It is then updated whenever an attempt is made to dispense a submunition or in the event of dispenser failure.

The binary variable used to construct the martingale is that of a successful / unsuccessful submunition dispense. If a submunition is dispensed as intended the martingale would be incremented by 1 - (rel_d.rel_s) (occurring with a probability of rel_d.rel_s). However, if a submunition failed to work (this would happen with a probability rel_d.(1 - rel_s) ), the martingale would be incremented by 0 - rel_d.rel_s representing the failure.

The only other case to consider now is that of dispenser failure -- this occurs with probability (1 - rel_d) and may be regarded as the combined failure of n_s submunitions. Hence the martingale increment in this case is n_s.(0 - rel_d.rel_s).

It is easy to show that the expected value of this martingale is zero simply by considering the martingale increment for each event, multiplying by the expected number of submunitions affected and summing over all events.

Detection/Hit/Kill martingales

For completeness, detection/hit/kill martingales were constructed for all target types using binary variables indicating the success or failure of each event. However due to the nature of the input data / program some of these were of no use. For example, where the probability of some event occurring is p=1.0 the martingale increment will always be 1-p=0.0, hence its sum will always be zero.

The remaining martingales reflected the "luck" in detection/hits/kills of certain targets. These were found to produce variance reductions (see table 1) in parameter 1 and especially in parameter 2.

Aircraft position (Control Variable)

A Normal[0,1] variable is selected by the program to give random variation on the aircrafts position relative to the target array. By using this as a control variable along with the above martingales, variance reductions of up to 50% in parameter 2, and 35% in parameter 1, were observed. Since this variable was common to all weapon systems within the model, it could have been applied, without any modification, to other systems and expected to give similar variance reductions.

The other control variables listed in table 1 were found to cause small variance productions for the base case and, as a result, were not adopted. [Note that tables 1, 2 and 3 give variance reductions achieved using both standard regression and the more robust jackknifed regression.]

Using this set of martingales and control variables, a number of tests were performed simply by varying some of the input parameters of the model. A summary of the variance reductions obtained in these tests is given in table 2.

By using standard regression to estimate the control variable coefficients, variance reductions on parameter 1 ranged from a small 1.0% up to a very good 56.7%, with an average of around 25%. Ashford and Beales cross-estimation test[6] revealed that the bias in the estimates of parameter 1 was very small and that it was not significant. Although, on average, the more robust jackknifed regression provided marginally greater variance reductions there is no reason to believe that this will always be the case. In fact, in just over half of the tests it was found to produce slightly worse variance reductions.

The variance reductions achieved for parameter 2 were considerably higher than for parameter 1. Although typically around 50%, variance reductions were observed from a very reasonable 25.9% up to an excellent 75.6% using standard regression. Again, bias was very small and not significant, and jackknifed regression provided similar reductions in variance. The main reason for the large variance reductions in parameter 2 compared to parameter 1 was that one of the martingales used was strongly-correlated with it -- refer back to table 1.

Although parameter 3 was one of the main parameters of interest, the variance of its estimate was smaller than that of parameters 1 and 2. Consequently it was already estimated to a sufficiently high degree of accuracy, and therefore was not of great importance when looking for control variables. None of the martingales or control variables looked at were particularly well-correlated with this parameter -- hence the variance reductions observed on it were small (see table 2).

Table 2. Control Variates Variance Reductions

A few examples with the model of weapon system 1*

                               PARAMETER 1    PARAMETER 2    PARAMETER 3
Input parameters varied        std.  jack-    std.  jack-    std.  jack-    n
                                    knifed         knifed         knifed

Base Case                      67.5   67.8    72.0   72.4    +1.1   +0.3  999

Random number seed             66.9   66.9    70.5   70.6    +1.1   +0.4  558
Attack angle                   72.6   72.1    81.1   80.7    +0.5   +0.2  590
Attack angle                   71.5   71.2    75.0   74.6    +0.3   +1.0  593
Kill probability               65.6   65.6    70.3   70.3    +2.0   +0.8  534
Target speed, attack angle     73.4   73.1    83.2   82.9    +1.5   +0.6  548
Target speed, attack angle     85.5   85.3    85.9   85.6    +1.8   +1.1  573
Target separation              67.1   68.4    70.5   71.9    -2.7   -0.1  564
Target separation              78.6   77.6    82.8   81.8    +0.8   -1.1  560
Ranging errors                 29.0   26.7    74.2   73.5    +0.9   +0.1  572
Terrain                        67.0   66.6    72.4   72.3    +1.5   +0.6  787
Attack angle                   42.8   42.9    54.8   54.7    -0.4   -1.1  579
Target array 1                 69.5   69.2    70.7   70.6    +1.4   -0.1  592
Target array 2                 54.1   54.8    58.9   59.8    -1.8   -1.7  566
Target array 3                 49.8   48.7    59.5   59.5    -0.2   +1.6  569
Target array 4                 53.1   52.8    61.3   61.2    +0.2   -0.2  567
Target array 5                 66.9   67.3    71.1   71.2    +5.8   +4.2  581
Ranging errors, terrain,
                attack angle    8.9    7.7    60.6   60.2    +1.7   +1.0  765
Ranging errors, terrain,
                attack angle    5.9    3.0    62.7   61.8    -0.4   +0.2  245

Mean variance reductions
                (19 runs)      57.7   57.2    70.4   70.3    +0.8   +0.4

* The control variables used for these tests consisted of: 1 dispenser/submunition martingale, 6 detection/hit/kill martingales, and 2 control variables for the aircraft's position.

By looking at the coefficients generated from the regression analysis it is possible to gain a greater insight as to what influences the models outcomes. It is also useful in that any peculiarities or irregularities in the model may be highlighted by strange coefficients. For example, suppose the dispenser/submunition reliability martingale was given a negative coefficient. This would suggest that the greater the number of submunitions successfully released, the lower the expected number of target hits! Clearly this is not what we would expect. By examining the coefficient obtained from the regression we should see this, in which case it would be necessary to seek some explanation of why this negative correlation has arisen.

APPLICATION TO OTHER WEAPON SYSTEMS

All martingales and control variables described in the previous section were chosen because they were relevant to any scenario of the model of weapon system 1 and were generally applicable to any other weapon system. For example, every weapon system will have associated detect/hit/kill probabilities, and also some form of dispenser / submunition combination with associated reliabilities. As mentioned above, the aircraft position control variable was common to all weapon systems.

Using this general set of martingales / control variables as a starting point, we could expect to achieve similar variance reductions for other weapon system models. It would then be possible, perhaps even desirable, to look at individual weapon system models and identify any weapon-system-dependent martingales or control variables. Further variance reductions would then be possible.

As an example it was decided to look at another weapon system model (referred to here as weapon system 2). The general set of martingales and control variables discussed previously was implemented and variance reductions only slightly less (on average) were observed. After looking at the model in more detail, a further two martingales were constructed from acceptance probabilities. These were similar to the detection martingales but involved the acceptance of targets once detected.

The variance reductions achieved with the addition of these two new martingales were now almost the same as those achieved for weapon system 1 -- compare tables 2 and 3. The most significant difference however was that variance reductions in excess of 50% were observed for parameter 3 where previously there had been almost none. This was due to the fact that just one of the two extra martingales was very relevant to this parameter whereas others used were only vaguely related.

Table 3. Control Variates Variance Reductions

A few examples with the model of weapon system 2*

                               PARAMETER 1    PARAMETER 2    PARAMETER 3
Input parameters varied        std.  jack-    std.  jack-    std.  jack-    n
                                    knifed         knifed         knifed

Base Case                      15.6   18.1    39.1   41.0    46.8   47.5  609

Random number seed             23.7   25.8    40.6   42.5    46.2   46.1  630
Attack angle                   50.3   51.3    64.9   64.1    38.8   38.3  620
Attack angle                   18.5   16.9    45.7   44.3    50.6   49.7  599
Kill probability               18.8   21.4    36.8   37.7    51.8   51.5  588
Target speed, attack angle     53.7   54.1    69.2   69.4    40.5   41.0  620
Target speed, attack angle      8.8    9.2    38.2   38.2    50.8   50.3  606
Target separation              30.8   31.5    44.3   44.7    50.5   49.3  592
Target separation              40.3   42.7    52.9   54.3    50.4   50.5  615
Ranging errors                 18.8   18.1    53.2   52.8    48.1   47.2  608
Terrain                        33.2   32.9    46.9   46.4    50.7   50.3  786
Attack angle                   15.6   18.1    39.1   41.0    46.8   47.5  609
Target array 1                 27.3   28.3    45.4   46.1    40.6   38.0  597
Target array 2                 11.0    8.7    30.3   28.1    44.7   45.1  612
Target array 3                  4.6    5.6    35.7   36.4    47.2   47.1  648
Target array 4                 16.4   16.4    34.9   35.2    47.0   47.2  602
Target array 5                 24.5   28.3    44.3   47.6    27.9   27.0  606
Ranging errors, terrain,
                attack angle   14.1   15.2    46.1   47.5    48.2   48.8  814
Ranging errors, terrain,
                attack angle   13.7   13.0    45.9   45.9    45.4   46.2  306

Mean variance reductions
                (19 runs)      23.1   24.0    44.9   45.4    45.9   45.7

* The control variables used for these tests consisted of: 1 dispenser/submunition martingale, 8 detect/accept/hit/kill martingales, and 1 control variable for the aircraft's position.

CONCLUSIONS

The antithetic variates Variance Reduction Technique is not really suited to large, complex simulation models such as those studied here. A simple modification to the technique is proposed to enable it to produce good variance reductions on more complex models. This does, however, depend on the main source of variation being in the latter stages of the simulation and whether this can be successful identified. The modified antithetic variates technique was applied to a large scale model, but gave similarly poor results to the full technique. The main reason behind its failure was that the main source of variation had not been identified at this stage.

A set of martingales and control variables -- generally applicable to all weapon system models -- were identified. They were found to give good variance reductions on the two models to which they were applied -- reductions in variance of up to 85% were observed for one parameter.

Two model-dependent martingales were constructed for the weapon system 2 model and gave further variance reductions.

The successful application of martingales and control variates, and indeed many other VRTs not considered here, relies upon a good understanding of the model. In this application, previous work on a similar, but more complex model proved to be very constructive, even though the variance reductions observed then were by no means as significant. This goes to show that for some types of simulation it is potentially very difficult to achieve good variance reductions.

Finally, the application of martingales and control variates to the large scale simulation models studied here was a great success. The author strongly recommends the application of these techniques to large scale simulation models when a reduction in variance is required.

Acknowledgement -- I should like to thank Dr. Robert Ashford of the University of Warwick for his helpful comments and suggestions both in this work and in writing this paper.

REFERENCES

[1] GOULD, S.R. (1989), The Effectiveness of Variance Reduction Techniques Applied to the Simulation of Air-to-Ground Line-of-Sight Engagements, Unpublished MOD(PE) Report

[2] HAMMERSLEY, J.M. and MORTON, K.W. (1956), A new Monte Carlo technique : antithetic variates, Proc. Camb. Phil. Soc. 52, 449-475

[3] KAHN, H. (1950), Random Sampling (Monte Carlo) Techniques in Neutron Attentuation Problems, Nucleonics 6(5), 6(6)

[4] KAHN, H. and MARSHALL A.W. (1953), Methods of Reducing Sample Size in Monte Carlo Computations, Opns. Res. 1(5), 263-278

[5] LAVENBERG, S.S. and WELCH, P.D. (1981), A Perspective on the Use of Control Variables to Increase the Efficiency of Monte Carlo Simulations, Mgmt. Sci. 27, 322-335

[6] ASHFORD, R.W. and BEALE, E.M.L. (1989), A Cross-Estimation Technique for using Control Variables in Stochastic Simulation, Eur. J. Opl. Res. 40, 352-362

[7] ASHFORD, R.W. and BEALE, E.M.L. (1989), Using Martingales to make Stochastic Simulations More Precise, Eur. J. Opl. Res. 38, 86-93

Feedback

So, what did you think? This is just a draft of this paper and I would appreciate any comments or feedback you may have. Please send comments via e-mail to the author.

*** DRAFT *** Variance Reduction Techniques applied to large scale simulation models

Table of Contents: